نکته مهم : همانطور که از مثال بالا می بینید در یک دبناله مهم نیست که ترتیب جملات و عناصر چگونه باشد ، ممکن است دنباله صعودی باشد و یا ممکن است نزولی باشد و شاید هم یک دنباله ای از عناصر متناوب باشد مانند مثال بالا.

شباهت دنباله با مجموعه ها :

اگر دقت کنید دنباله ها و مجموعه ها شباهتهایی دارند به غیر از دو مورد :

۱-ترتیب در نمایش دنباله ها مهم است اما در نمایش مجموعه ها مهم نیست .

۲-در دنباله ها ما می توانیم مقادیر مشابه را داشته باشیم و این مقادیر مفهوم خاص دارند ، اما در مجموعه ها مقادیر مشابه و مساوی مفهوم خاص ندارند و کلا یکسان هستند .به عنوان مثال:

دنباله {۰،۱،۰،۱،۰،۱،۰،۱} مفهوم یک دنباله متناوب متناهی است . اما همین در مجموعه ها برابر با {۰،۱} خواهد بود .

قانون دنباله ها :

دنباله ها معمولا دارای یک قانون هستند .این قانون یا ضابطه ، نشان دهنده نظم و ترتیبی که بین عناصر دنباله وجود دارد .

فرمول دنباله یا جمله عمومی دنباله:

ما تا الان دانستیم که دنباله ها ، دارای ارتباط و ضابطه بین عناصر خود هستند ، خیلی مهم است که ما این ضابطه موجود در یک دنباله را بدانیم چرا که در دنباله های نا متناهی باعث می شود ما براحتی بتوانیم جملات دنباله را بدست آوریم . مثلا ۱۰ مین عنصر دنباله و یا شاید هزارمین عنصر دنباله هم لازم باشد . خوب طبیعی است اینجا ما باید حتما فرمول دنباله را داشته باشیم .

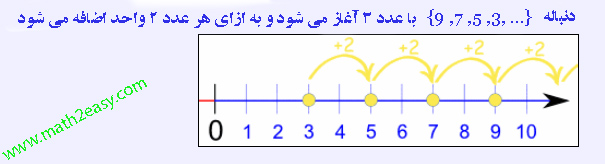
مثال : ما دنباله ای داریم از عناصر {….،۳،۵،۷،۹ } خوب ضابطه این دنباله چیست ؟ جمله صدم این دنباله چیست ؟

جواب : ما با یک نگاه حدس می زنیم که بین هر دو عدد ما به اندازه ۲ واحد پرش داریم در واقع هر عدد نسبت به عدد قبلیش ۲ واحد اضافه شده است . پس ما حدس می زنیم قانون کلی ۲n  باشد . الان طبق جدول زیر امتحان می کنیم و نتیجه را می بینیم :

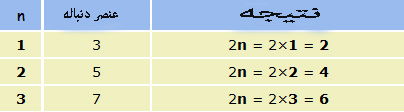
خوب طبق جدول بالا ما تقریبا به جواب رسیدیم اما نتیجه  فرمول ما یک واحد کم دارد یعنی باید برای هر جمله یک واحد دیگر اضافه کنیم تا همان جملات دنباله بدست آید . پس باید فرمول دنباله ما ۲n+1  باشد.

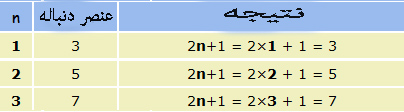
اکنون به  جدول بالا نگاه کنید اکنون ما فرمول درست را بدست آوردیم . پس اکنون براحتی می توانیم جمله صدم دنباله را نیز حساب کنیم .

و سرانجام :

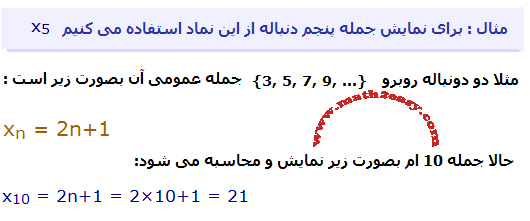
برای نمایش حالت کلی فرمول و قانون یک دنباله از فرمول کلی زیر استفاده می کنیم :